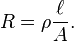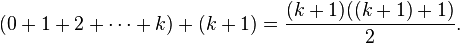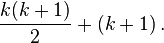The wikipedia says about mathematical induction:
Mathematical induction is a method of
mathematical proof typically used to establish that a given statement is true for all
natural numbers (positive
integers). It is done by proving that the
first statement in the infinite sequence of statements is true, and then proving that if
any one statement in the infinite sequence of statements is true, then so is the
next one.
Example
Mathematical induction can be used to prove that the following statement, which we will call P(n), holds for all natural numbers n.

P(
n) gives a formula for the sum of the
natural numbers less than or equal to number
n. The proof that
P(
n) is true for each natural number
n proceeds as follows.
Basis: Show that the statement holds for n = 0.
P(0) amounts to the statement:

In the left-hand side of the equation, the only term is 0, and so the left-hand side is simply equal to 0.
In the right-hand side of the equation, 0·(0 + 1)/2 = 0.
The two sides are equal, so the statement is true for n = 0. Thus it has been shown that P(0) holds.
Inductive step: Show that if P(k) holds, then also P(k + 1) holds. This can be done as follows.
Assume P(k) holds (for some unspecified value of k). It must then be shown that P(k + 1) holds, that is:
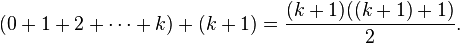
Using the induction hypothesis that P(k) holds, the left-hand side can be rewritten to:
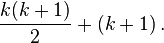
Algebraically:

thereby showing that indeed P(k + 1) holds.
Since both the basis and the inductive step have been proved, it has now been proved by mathematical induction that P(n) holds for all natural n
here is another example by me:























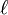 is the length of the piece of material (measured in
is the length of the piece of material (measured in