The wikipedia says about mathematical induction:
Mathematical induction is a method of mathematical proof typically used to establish that a given statement is true for all natural numbers (positive integers). It is done by proving that the first statement in the infinite sequence of statements is true, and then proving that if any one statement in the infinite sequence of statements is true, then so is the next one.
The method can be extended to prove statements about more general well-founded structures, such as trees; this generalization, known as structural induction, is used in mathematical logic and computer science. Mathematical induction in this extended sense is closely related to recursion.
Example
Mathematical induction can be used to prove that the following statement, which we will call P(n), holds for all natural numbers n.
P(n) gives a formula for the sum of the natural numbers less than or equal to number n. The proof that P(n) is true for each natural number n proceeds as follows.
Basis: Show that the statement holds for n = 0.
P(0) amounts to the statement:
P(0) amounts to the statement:
In the left-hand side of the equation, the only term is 0, and so the left-hand side is simply equal to 0.
In the right-hand side of the equation, 0·(0 + 1)/2 = 0.
The two sides are equal, so the statement is true for n = 0. Thus it has been shown that P(0) holds.
In the right-hand side of the equation, 0·(0 + 1)/2 = 0.
The two sides are equal, so the statement is true for n = 0. Thus it has been shown that P(0) holds.
Inductive step: Show that if P(k) holds, then also P(k + 1) holds. This can be done as follows.
Assume P(k) holds (for some unspecified value of k). It must then be shown that P(k + 1) holds, that is:
Using the induction hypothesis that P(k) holds, the left-hand side can be rewritten to:
Algebraically:
thereby showing that indeed P(k + 1) holds.
Since both the basis and the inductive step have been proved, it has now been proved by mathematical induction that P(n) holds for all natural n
here is another example by me:












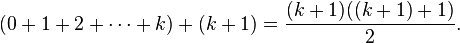
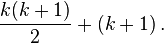


0 comments:
Post a Comment